This article is a continuation of the Neo4j database series. If you are coming here directly and not familiar with Neo4j database & Cypher query language, read these articles first.
Graph is a very popular and well established data structure/model in computer science, and it has practical application in many domains from data science, research, social networks, e-commerce & logistics to biology and more.
Among the very popular application of graphs in everyday life, one is routing or navigation systems. In a navigation systems (for example, maps) all the points are the routes between them are perfectly represented with vertices and edges of a graph. Then different traversal algorithms like DFS or BFS are applied to solve specific routing problems.
Routing problems apply not only to maps, but also to data networks, social media and many other types of applications. Here, we’ll look at a set of problems commonly known as shortest path problems, and see how easily they can be solved with neo4j database and cypher queries.
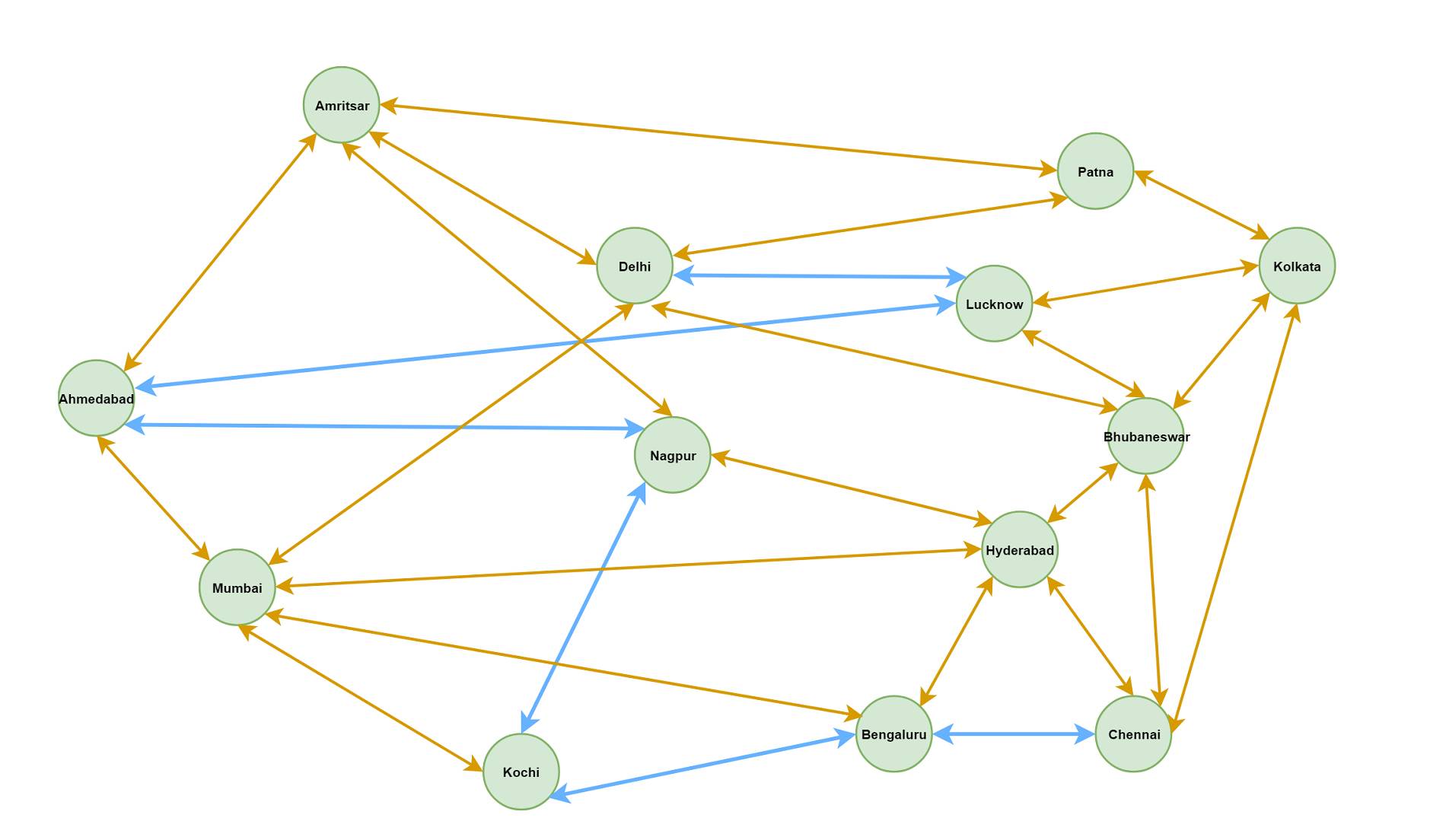
A map of Indian cities
To demonstrate the problem, we’ll use a simplified (not-so-real) map of few Indian cities. The cities are connected with roads.
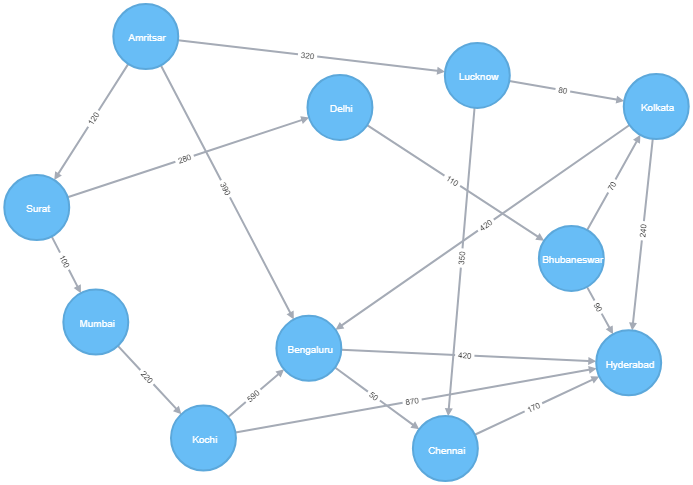
First we’ll need to setup the map with cities (nodes) and roads (relationships). The data is available as CSV files, one for the cities and the other for roads. We’ll use the load CSV feature to load the data.
The cities.csv file has 2 columns, Id and Name but no headers. The roads.csv file has 4 columns and has headers in first row. The columns are Id, FromCity, ToCity & DistanceKM. The Id from first file is used to map the cities in the second file (like FK-PK relationship). We use the Id from the second file to generate names for the roads as NH-{Id} since this Id is not referenced anywhere else.
Below Cypher queries read the CSV files and load them into neo4j as nodes (:City) and relationships [:LINK]. Note that we are using local files here, and for that to work the files need to be saved inside the /neo4j_root/import directory. We could also refer the files from some http location.
//Q1 - read cities and load them as nodes in DB (file has no headers)
LOAD CSV FROM "file:///cities.csv"
AS line
CREATE (:City { id: toInteger(line[0]), name: line[1] })
//Q2 - read the roads, map to cities and load as relationships
LOAD CSV WITH HEADERS FROM "file:///roads.csv"
AS line
MATCH (c1:City { id: toInteger(line.FromCity) }),
(c2:City { id: toInteger(line.ToCity) })
CREATE path = (c1) -[:LINK {name: 'NH-' + line.Id, distance: toInteger(line.DistanceKM) }]-> (c2)
Once the queries are run successfully, we get the complete map as a graph.
Shortest path
Cypher as a built-in shortestpath() function. We’ll use that to find the shortest path between 2 cities viz. Amritsar and Hyderabad. We use a variable length pattern matching to get all possible roads from Amritsar to Hyderabad and then use the function to get the shortest one. See query below.
//Q3 - in-built shortest-distance = minimum hops
MATCH (c1:City {name: "Amritsar"}),
(c2:City {name: "Hyderabad"}),
path = shortestpath((c1)-[:LINK*]-(c2))
RETURN path
It returns the path “Amritsar –> Bengaluru –> Hyderabad”, with a total distance of 810km.
Note that it returns the shortest path that has minimum number of hops. It does not take the distance into calculation. This is the behaviour of the default shortestpath() function and no custom property is used for the calculation.
This is definitely not be the best solution for a map navigation problem, as the “shortest path” is not actually the shortest one as per our distance property is concerned. But this is very useful in lot of situations like calculation the most efficient path to deliver data packets over a wired network (with minimum hops) or figuring out closest relation between two persons on a social network.
Weighted shortest path - distance
Now let’s solve the original problem of shortest distance between 2 cities. What we do here is, find out all possible routes between the two then take the shortest one by distance. We use REDUCE to calculate the total distance in a route.
//Q4 - actual shortest-distance
MATCH (source:City {name: "Amritsar"}), (destination:City {name: "Hyderabad"}),
path = (source) -[road:LINK*]- (destination)
WITH path, REDUCE (sum = 0, r IN road | sum + r.distance) AS dist
ORDER BY dist
LIMIT 1
RETURN path
We can format the result a bit with cities passed through, the roads traversed (remember, they are named like NH-1 etc.) and the total distance. The head() function takes the first item in a list and tail() takes all but the first.
//Q5 - with formatted result set
MATCH path = (:City {name: "Amritsar"}) -[road:LINK*]- (:City {name: "Hyderabad"})
WITH path, REDUCE (sum = 0, r IN road | sum + r.distance) AS dist
ORDER BY dist
LIMIT 1
RETURN REDUCE (cities = head(nodes(path)).name, n IN tail(nodes(path)) | cities + '->' + n.name) AS Route,
REDUCE (rd = head(relationships(path)).name, r IN tail(relationships(path)) | rd + ' > ' + r.name) AS Roads,
dist + ' km' AS Distance
It produces the following results:
Route: Amritsar->Lucknow->Kolkata->Bhubaneswar->Hyderabad
Roads: NH-1 > NH-4 > NH-9 > NH-10
Distance: 560 km
Note: Understand that this query works fine even with unlimited number of hops (see -[road:LINK*]-) because the size of the graph is very small. When there are millions of nodes in the graph, this query will not be practical, and we might have to restrict the paths within a range of hops like -[road:LINK*1..n]- with a reasonable value of n or look for other alternatives.
Note: Here we have considered all the roads are two-way i.e. if there is a road from Delhi to Bhubaneswar, there is also a return way from Bhubaneswar to Delhi. If that is not true, and roads are one-way as shown in the graph diagram, we just need to make the MATCH pattern have a directed relationship to solve it. Now, when we make the MATCH pattern directed ()-[:LINK]->(), we get most common variant of Dijkstra’s algorithm solved.
With road blocks
In real life, many a times we face a situation where there are road blocks. How do we improve our solution for those situations? Let’s first block some roads. We just randomly block two roads NH-3 and NH-4 (between Amritsar-Bengaluru and Lucknow-Kolkata). We add a new property isBlocked: true to mark a road as blocked.
//Q6 - adding road blocks
MATCH () -[r:LINK]-> ()
WHERE r.name IN ['NH-3', 'NH-4']
SET r.isBlocked = true
Now to upgrade the query to consider the road blocks, we filter out and include only the routes where none of the roads are blocked.
//Q7 - navigating around road blocks
MATCH path = (:City {name: "Amritsar"}) -[road:LINK*]- (:City {name: "Hyderabad"})
WHERE ALL (r IN road WHERE NOT exists(r.isBlocked)) //all roads are non-blocked
WITH path, REDUCE (sum = 0, r IN road | sum + r.distance) AS dist
ORDER BY dist
LIMIT 1
RETURN REDUCE (cities = head(nodes(path)).name, n IN tail(nodes(path)) | cities + '->' + n.name) AS Route,
REDUCE (rd = head(relationships(path)).name, r IN tail(relationships(path)) | rd + ' > ' + r.name) AS Roads,
dist + ' km' AS Distance
It produces the following results:
Route: Amritsar->Surat->Delhi->Bhubaneswar->Hyderabad
Roads: NH-2 > NH-6 > NH-8 > NH-10
Distance: 600 km
With traffic
Let’s now make it even more realistic with traffic. In real life, many a times, we want the “fastest route” rather than the “shortest route”. The average speed on a road might vary because of traffic, road conditions and other factors. To simulate the situation, we introduce a new property to the roads as average speed.
First we clean up the map, reload the cities and load the roads from a new CSV that associates an average speed with each road link. In the query, we add a new property avgSpeed to the [:LINK] relationship with float values.
//Q8 - delete the whole map
MATCH (n) DETACH DELETE n
//run Q1 again to load the city nodes
//Q9 - load the roads with average speed from new file
LOAD CSV WITH HEADERS FROM "file:///roads2.csv"
AS line
MATCH (c1:City { id: toInteger(line.FromCity) }),
(c2:City { id: toInteger(line.ToCity) })
CREATE path = (c1) -[:LINK {avgSpeed: toFloat(line.SpeedKmph), name: 'NH-' + line.Id, distance: toInteger(line.DistanceKM) }]-> (c2)
//run Q6 to add the road blocks
With our new roads (i.e. [:LINK] relationships) with property avgSpeed, we can calculate the fastest route using similar logic, only we choose route with minimal travel time than distance. Just for a comparison, we’ll print out all the possible routes with in order of travel time. Also, we used directed paths for this query. Results are shown below.
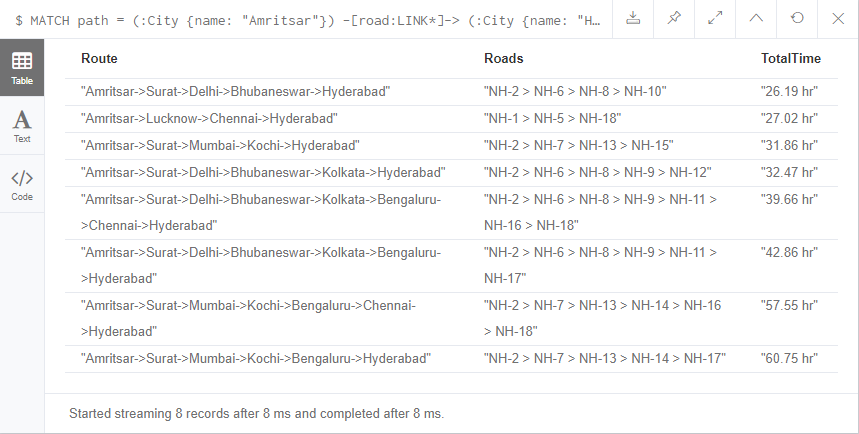
//Q10 - fastest route
MATCH path = (:City {name: "Amritsar"}) -[road:LINK*]-> (:City {name: "Hyderabad"})
WHERE ALL (r IN road WHERE NOT EXISTS (r.isBlocked))
WITH path, REDUCE (sum = 0, r IN road | sum + (r.distance / r.avgSpeed)) AS time
ORDER BY time
RETURN REDUCE (cities = head(nodes(path)).name, n IN tail(nodes(path)) | cities + '->' + n.name) AS Route,
REDUCE (rd = head(relationships(path)).name, r IN tail(relationships(path)) | rd + ' > ' + r.name) AS Roads,
toString((round(time * 100))/100) + ' hr' AS TotalTime
This concludes this post and we have seen some variations of practical shortest path problems, form minimum hops to shortest path by distnace, and then avoiding road blocks and traffic. Though these are over-simplified examples, and may not be applicable to solve real life problems within practical limits, they should give some idea on how to use Neo4j database and Cypher queries to solve problems in different graph-related problems.
Note: I’ll publish another post in the Neo4j series and discuss about some common considerations for production deployment of Neo4j. Do come back later for the next post.
comments powered by Disqus